Plano de Aula de Geografia
(7° Ano) – Gráficos de setores e de colunas: analisando a população do
Centro-Oeste
Objetivo de aprendizagem
Identificar
características sociais e econômicas da Grande Região Centro-Oeste por meio da
construção de gráficos de colunas e de setores.
Objeto de conhecimento: Mapas temáticos do Brasil.
Habilidade trabalhada: (EF07GE10) Elaborar e interpretar gráficos
de barras, gráficos de setores e histogramas, com base em dados socioeconômicos
das regiões brasileiras.
Tempo estimado
2 aulas
Recursos didáticos
·
Folhas de
papel quadriculado, folhas de papel sulfite A4, régua, lápis de cor e
transferidores de 360°.
Desenvolvimento da
sequência didática
Aula 1
Organize a turma em
semicírculo, de modo que a lousa fique disponível para anotações. Informe aos
alunos que a aula terá como tema os usos, a construção e a leitura de gráficos
de setores e de colunas.
Inicie explicando que a
Geografia lida com muitos dados estatísticos: população absoluta, população
relativa, taxas de natalidade e de mortalidade, crescimento econômico etc.
Muitas vezes, esses dados precisam ser comparados a outros ou analisados em uma
sequência temporal. Para facilitar a apresentação e análise dessas informações,
empregam-se diversos tipos de gráfico, entre os quais o de setores e o de colunas.
O gráfico de setores
(também conhecido como gráfico de “pizza” ou circular) é construído a partir de
uma circunferência que representa uma totalidade. Essa totalidade é repartida
em categorias, e cada setor (ou fatia) do gráfico se refere à proporção dessa
categoria em relação ao todo. Por exemplo: se na sala de aula há 30 alunos e,
entre esses, há 18 meninas e 12 meninos, podemos usar a circunferência completa
para representar o universo de estudantes da classe e reparti-la de modo a
representar a proporção de meninas e meninos dentro desse total. Enfatize que
esse tipo de gráfico em geral trabalha com valores percentuais. Assim, os 30
alunos corresponderiam a 100%, a proporção de meninas seria de 60% e a
proporção de meninos seria de 40%. Nesse momento, se preferir, use o número
real de meninas e meninos na turma e construa um gráfico de setores na lousa.
Os alunos deverão notar que esse tipo de representação gráfica permite perceber
mais facilmente se há predomínio de uma ou outra categoria.
Em seguida, apresente o
gráfico de colunas. Explique que se trata de um gráfico bastante versátil:
entre outros usos, ele pode servir para demonstrar a proporção de categorias
dentro de um universo (como no exemplo do total de alunos da classe e a
proporção de meninos e meninas) ou para comparar uma série histórica de dados
(por exemplo, o número de alunos do sétimo ano na escola ao longo dos anos).
Construa na lousa um
exemplo de gráfico de colunas. Uma possibilidade é solicitar o estojo de um dos
estudantes, contabilizar seus itens e expor os dados em forma de gráfico – por
exemplo, uma régua, duas canetas azuis, uma caneta vermelha, dois lápis, uma
borracha e um apontador. Demonstre que a representação dessa informação na
forma de gráfico permite identificar de maneira simples e rápida quais objetos
há no estojo em maior ou menor quantidade. Outra possibilidade é construir um
gráfico representando uma série temporal – como a média da turma na disciplina
de Geografia nas três últimas avaliações. Nesse caso, enfatize que o gráfico
permite verificar tendências, como a ascensão ou a queda das médias.
Dê esclarecimentos sobre
os procedimentos de leitura do gráfico de colunas. Explique que é necessário
identificar o tipo de informação que os eixos apresentam lendo os rótulos que
os acompanham. Em seguida, é preciso estabelecer uma correspondência entre a
altura da coluna e o valor associado a essa altura no eixo vertical do gráfico.
É importante que os alunos
compreendam que o uso de gráficos não está limitado ao ambiente escolar: há
muitas situações cotidianas em que dados numéricos são apresentados dessa
forma. Por esse motivo, aprender a ler e interpretar gráficos é uma
aprendizagem importante. Fundamente essa argumentação com exemplos de uso de
gráficos no dia a dia das pessoas. Se for possível, organize e apresente
exemplos de gráficos extraídos de jornais, revistas e outros documentos que
possam fazer parte da rotina dos estudantes.
Ao final da aula, elabore
um esquema na lousa para registrar os tópicos principais da aula. Uma forma de
elaborar esse esquema é escrever a palavra “gráfico” no centro da lousa e criar
elementos de ligação (linhas ou setas) indicando os aspectos tratados: tipos de
gráfico, importância, uso, procedimentos de leitura etc. Proponha aos alunos
que registrem o esquema no caderno.
Aula 2
Antecipadamente,
providencie os materiais necessários para a aula: folhas de papel quadriculado,
folhas de papel sulfite A4, régua, lápis de cor e transferidores de 360°.
Organize a turma em cinco grupos. Garanta que cada aluno do grupo tenha os
materiais necessários para a construção de um gráfico de setores e um gráfico
de colunas.
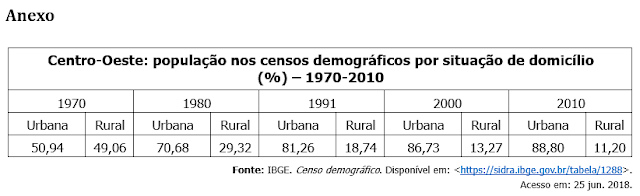
Inicie escrevendo na lousa
os dados da tabela em anexo. Faça a leitura da tabela com os alunos. Destaque
que os dados apresentados foram obtidos nos Censos Demográficos realizados pelo
IBGE e permitem analisar a evolução da população urbana e rural do Centro-Oeste
de 1970 a 2010. Associe os dados a conteúdos que tenham sido trabalhados no
estudo dessa Grande Região.
Explique que cada grupo
ficará responsável por representar os dados referentes a um dos anos do período
contemplado na tabela. Assim, um grupo ficará com os dados de 1970, outro com
os dados de 1980, e assim por diante.
Nesse momento, informe os
procedimentos para a construção do gráfico de setores. Explique aos alunos que
deverão usar o transferidor para desenhar uma circunferência sobre a folha de
sulfite. Depois, eles deverão calcular o tamanho do setor que vai representar a
proporção referente à porcentagem de população rural e urbana. Para isso, devem
considerar que a circunferência tem 360°, que representam 100%. Dividindo-se
360° por 100, percebemos que a cada 3,6° na circunferência teremos 1% do total
do universo. Assim, o próximo passo é multiplicar as porcentagens relativas à
população rural e à população urbana por 3,6. Por exemplo, no caso do ano de
1970, 50,94% da população era urbana. Para representar essa proporção na
circunferência, deve-se multiplicar 50,94 por 3,6. O resultado da conta é
183,38. No caso da população rural, deve-se multiplicar 49,06 por 3,6. O
resultado é 176,6. Para facilitar, oriente os alunos a arredondar os resultados
para 183 e 177.
Feitos esses cálculos, os
alunos devem usar o transferidor para determinar o centro da circunferência e,
em seguida, localizar o ponto correspondente a 183°, também com a ajuda do
transferidor. Com uma régua, eles devem traçar uma linha reta entre esse ponto
e o centro da circunferência. O próximo passo é somar 177 a 183. O resultado
será 360. Assim, uma reta deve ser traçada do ponto correspondente a 360° (que
corresponde ao zero do transferidor) até o centro da circunferência. Após esses
procedimentos, a circunferência ficará dividida em duas partes. Solicite aos
alunos que pintem cada parte de uma cor e que construam uma legenda associando
as cores às informações que elas representam. Por fim, oriente-os a incluir um
título e a fonte dos dados do gráfico.
Passe então à construção
do gráfico de colunas. Oriente os alunos a traçar no papel quadriculado dois
eixos perpendiculares. Defina antecipadamente a escala mais adequada,
considerando os valores da tabela. Uma possibilidade é iniciar o eixo vertical
no zero e determinar que as porcentagens sejam inseridas com um intervalo de
dez pontos percentuais. Após traçar os eixos do gráfico, os alunos devem usar a
régua para construir uma coluna com altura correspondente à porcentagem da
população rural e outra da população urbana. Por fim, devem pintar cada coluna
de uma cor e construir uma legenda que identifique as informações representadas
pelas cores. O título e a fonte também devem ser inseridos.
Atividade complementar
Recolha todos os gráficos
e organize-os de acordo com a série histórica dos dados. Forme cinco conjuntos
de gráficos de 1970 até 2010. Entregue esses conjuntos aos grupos e peça que
analisem a evolução da população rural e urbana no Centro-Oeste. Para isso,
elabore algumas perguntas que norteiem a análise, por exemplo:
·
A população
urbana aumentou ou diminuiu entre 1970 e 2010?
·
A população
rural aumentou ou diminuiu entre 1970 e 2010?
·
Em que período
houve maior aumento da população urbana?
·
Que tendência
os dados apontam em relação à evolução da população rural e urbana no
Centro-Oeste?
·
Proponha aos
alunos que debatam as questões em grupo e elaborem um texto coletivo com as
conclusões a que chegaram.
Acompanhamento das
aprendizagens
O acompanhamento das
aprendizagens deve ocorrer de maneira contínua e se valer de todos os momentos
de interação com os alunos. Assim, é importante observar a pertinência das
perguntas feitas em classe, a forma como executam os registros no caderno e a
maneira como realizam as atividades propostas.
Para realizar o
acompanhamento das aprendizagens, aplique as propostas de avaliação e de
autoavaliação sugeridas a seguir.
Avaliação
Como proposta de avaliação,
verifique se os alunos conseguiram elaborar e interpretar os gráficos de
setores e de colunas. É importante observar se o procedimento de construção de
gráfico colaborou para capacitar o aluno a ler e interpretar informações nessa
forma de representação. Durante a atividade complementar, verifique se os
alunos conseguem comparar os gráficos e detectar tendências na evolução
populacional da Grande Região Centro-Oeste.
Para ampliar o processo de
avaliação, oriente-se pelas questões a seguir.
·
O aluno participou
das aulas expressando-se de forma educada e respeitando os momentos de fala do
professor e dos colegas?
·
O aluno é
capaz de trabalhar em grupo, negociando, argumentando e cedendo?
·
O aluno
aprendeu os procedimentos de construção de gráficos de setores e de colunas?
·
O aluno é
capaz de identificar informações em gráficos de setores e de colunas?
·
O aluno é
capaz de comparar diferentes gráficos e compreender a relação entre dados de
uma série histórica?































0 Comentários